Manual de Trigonometría Alberto Guadarrama: agosto 2016

Existen básicamente dos formas de definir un ángulo en el plano:

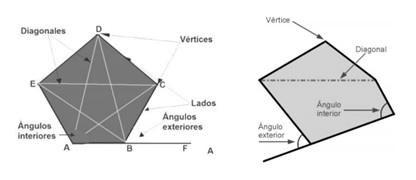
Forma Geométrica: Se denomina ángulo a la amplitud entre dos líneas que concurren en un punto común llamado vértice. El ángulo entre dos curvas es el ángulo que forman sus rectas tangentes en el punto de intersección.

Forma Trigonométrica: es la amplitud de rotación o giro que describe un segmento rectilíneo en torno a uno de sus extremos tomado como vértice desde una posición inicial hasta una final. Si la rotación es en sentido contrario a las manecillas del reloj, se considera positivo. De lo contrario se considera negativo. Este ángulo puede superar el orden de los 360º a diferencia del ángulo geométrico.

Sistemas de medición:

· Grado Sexagesimal
· Grado Centesimal
· Radian

Convertir

Clasificación de los ángulos

Ángulos formados por dos rectas paralelas y una secante

Esta configuración, da a origen a nueva clasificación llamandose:

- ángulos internos: Son 2 ángulos internos no adyacentes, ubicados a un lado distinto de la recta secante.

Como es el caso de los ángulos: 4 = 6, 3 = 5.

- ángulos extremos: Son 2 ángulos extremos no adyacente, ubicados a un lado distinto de la recta secante.

Como es el caso de los ángulos: 2 = 8, 1 = 7.

- ángulos opuestos por el vértice: Son ángulos que poseen en común un vértice y uno de los lados de sus ángulos.

Como es el caso de los ángulos: 2 = 4, 6 = 8, 1 = 3, 5 = 7.

- ángulos correspondientes: Son 2 ángulos no adyacentes, ubicados en un mismo lado de la secante, pero interno y externo.

Como es el caso de los ángulos: 2 = 6, 1 = 5, 3 = 7, 4 = 8.

- ángulos adyacentes (Suplementarios): Son aquellos ángulos que poseen un lado en común y unidos suman (180 grados sexagesimales).

Como es el caso de los ángulos: 6 + 3 = 180, 5 + 4 = 180.

- ángulos colaterales internos (Suplementarios): Son 2 ángulos internos no adyacentes ubicados a un lado distinto de la recta secante y unidos suman (180 grados sexagesimales).

Como es el caso de los ángulos: 7 + 2 = 180, 1 + 8 = 180.

- ángulos colaterales externos (Suplementarios): Son 2 ángulos externos no adyacentes ubicados a un lado distinto de la recta secante y unidos suman (180 grados sexagesimales).

Como es el caso de los ángulos: 1 + 2 = 180, 2 + 3 = 180, 3 + 4 = 180, 1 + 4 = 180, 5 + 6 = 180, 6 + 7 = 180, 7 + 8 = 180, 5 + 8 = 180.

Serie de Ejercicios

Determina el valor de los ángulos que se muestran en las siguientes figuras:

Congruencia y Semejanza de Triángulos

Congruencia:

Si un triángulo tiene todos sus lados y ángulos respectivamente iguales a los lados y ángulos del otro, se dice que son: Triángulos congruentes

Semejanza:

Se dice que las figuras geométricas que presentan la misma forma son semejantes, tratándose de triángulos se dice que son semejantes si tienen sus ángulos respectivos iguales y si sus lados correspondientes son proporcionales.

EJERCICIOS Y APLICACIONES DE SEMEJANZA

1. Cuenta la historia que el gran matemático griego Tales de Mileto midió la altura de las pirámides de Egipto usando un método muy simple: comparó la sombra de su bastón con la sombra de la pirámide. Si su bastón medía 1 metro y proyectaba una sombra de 50 cm. ¿cuál es la altura de una pirámide cuya sombra mide 45 metros? Explica tus cálculos usando un diagrama.

2. Las dimensiones de una fotografía son 6,5 cm. por 2,5 cm. Se quiere ampliar de manera que el lado mayor mida 26 cm. ¿Cuánto medirá el lado menor?

3. Un árbol de 3 metros de alto a una cierta hora genera una sombra de 1,8 metros de largo. ¿Cuánto medirá la sombra de una persona de 2 metros de alto a la misma hora?.

4. En un plano de una casa a escala 1:50, el comedor mide 12 cm. por 15 cm. Determina las dimensiones reales del comedor.

5. Se midió un terreno con una cinta métrica trucada de 50 m, dando un área de 90 Ha. Posteriormente, el comprador comprueba que la medida real de la cinta era de 49 m. ¿Será necesario volver a medir el terreno?. Si el precio de la Ha era de $400.000, ¿en cuánto se pretendía engañar al comprador?

Teorema de Tales

Como definición previa al enunciado del teorema, es necesario establecer que dos triángulos son semejantes si tienen los ángulos correspondientes iguales y sus lados son proporcionales entre si. El primer teorema de Tales recoge uno de los postulados más básicos de la geometría, a saber, que:

Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes.

Ejercicios:

Para aprender más...

Eratostenes y la medición del radio Terrestre

Triángulos

Definición: Porción del plano limitado por tres rectas que se intersecan una a una en puntos llamados vértices. Polígono de tres lados, tres ángulos y tres vértices.

Los triángulos son los únicos polígonos que no tienen diagonales.

A los triángulos también reciben el nombre de trígonos.

Clasificación

Puntos y Rectas Notables

MEDIANA: Es el segmento trazado desde un vértice al punto medio del lado opuesto; Es el segmento de recta que une a un vértice con el punto medio del lado opuesto.

BARICENTRO: Es el punto donde se cortan las medianas, es decir, el punto donde está aplicado todo el peso de un cuerpo triangular.

MEDIATRIZ: Es la perpendicular trazada en el punto medio de cada lado del triángulo.

CIRCUNCENTRO: Es el punto de intersección de las mediatrices de los lados de un triángulo.

ALTURA DEL TRIÁNGULO: Es el segmento de recta perpendicular trazada desde un vértice, al lado opuesto; Hay tres alturas, una correspondiente a cada lado.

ORTOCENTRO: Es el punto donde se cortan las tres alturas del triángulo.

BISECTRIZ: Es la semirrecta que divide al ángulo en dos ángulos congruentes ó iguales.

INCENTRO: Es el punto de intersección de las bisectrices de los ángulos interiores de un triángulo; Es el centro de la circunferencia inscrito en un triángulo.

Ingresa al siguiente link para interactuar:

http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena9/1quincena9_contenidos_2c.htm

Teorema de Pitágoras

El área del cuadrado construido sobre la hipotenusa de un triángulo rectángulo, es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.

c²= a² + b²

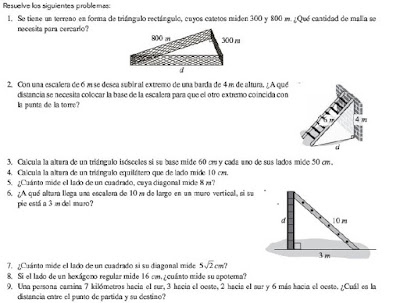
^Ejercicios:

Razones trigonométricas

^Ejercicios:

En los siguientes ejercicios, dada la función trigonométrica, expresa las funciones restantes en

relación con el ángulo dado. Traza el triángulo rectángulo correspondiente y utiliza el teorema

de Pitágoras para localizar los valores restantes.

Ejemplos de aplicación

Triángulos Oblicuángulos

Ley de Senos

Se utiliza cuando se conoce:

a) Dos ángulos y un lado opuesto

b) Dos lados y un ángulo opuesto

Ley de Cosenos

Se utiliza cuando se conocen:

a) Dos lados y el ángulo entre ellos

b) Los tres lados

Módulo 1 FIGURAS GEOMÉTRICAS

1 Definición de figura geométrica.

Se define como un conjunto no vacío que está compuesto por puntos y comprendidas como un lugar geométrico es un área cerrada por líneas o superficies, ya sea en un plano o en el espacio.

Figura geométrica. Extensión limitada por puntos, líneas y superficies

2 Clasificación de figuras geométricas:

Clasificación de los polígonos

Los polígonos se clasifican de acuerdo con sus lados o la magnitud de sus ángulos interiores.

Por sus lados

· Regulares. Tienen todos sus lados iguales.
· Irregulares. Tienen la medida de sus lados diferentes.

Por sus ángulos

· Convexo. Los ángulos interiores son todos menores que 180°
· Cóncavo. Uno de sus ángulos interiores es mayor que 180°.

3. Trazo de polígonos.

Definición de polígono

Se llama polígono a aquella figura plana cerrada, delimitada por segmentos de recta. Se clasifican de acuerdo con la medida de sus lados o sus ángulos. La palabra polígono proviene del griego POLYGONOS; de POLYS, que significa muchos y de GONIA que significa ángulos.

Elementos de un polígono:

· Vértice. Es el punto donde concurren 2 lados.
· Ángulo interior. Es el que se forma con 2 lados adyacentes de un polígono.
· Ángulo exterior. Aquel que se forma entre la prolongación de uno de los lados y su lado adyacente.
· Diagonal. Es el segmento de recta que une 2 vértices no adyacentes.

Número de diagonales

El número de diagonales totales en un polígono se obtendrá en función del número de lados.

Dónde:

D = diagonales totales del polígono.

n =número de lados

Número de diagonales trazadas desde un mismo vértice
En un polígono de n lados se pueden trazar (n – 3) diagonales desde un solo vértice, entonces la fórmula es:

d = n – 3

Donde:

d = diagonales trazadas desde un solo vértice.

n= número de lados

Ángulos de un polígono

La magnitud de los diferentes ángulos de un polígono se obtiene con las fórmulas siguientes: